discover variance utilizing Python

This article was initially revealed on Constructed In by Eric Kleppen.

Variance is a robust statistic utilized in knowledge evaluation and machine studying. It is without doubt one of the 4 fundamental measures of variability together with vary, interquartile vary (IQR) and commonplace deviation. Understanding variance is essential as a result of it provides you perception into the unfold of your knowledge and can be utilized to check variations in pattern teams or determine essential modeling options. Variance can be utilized in machine studying to know adjustments in mannequin efficiency on account of utilizing totally different samples of coaching knowledge.

Calculating variance is straightforward utilizing Python. Earlier than diving into the Python code, I’ll first clarify what variance is and how one can calculate it. By the tip of this tutorial you’ll have a greater understanding of why variance is a crucial statistic, together with a number of strategies for calculating it utilizing Python.

What’s variance?

Variance is a statistic that measures dispersion. Low variance signifies that values are usually related and don’t range extensively from the imply whereas excessive variance signifies values are extra extensively dispersed from the imply. You should utilize variance on both a pattern set or all the inhabitants because the calculation takes in all knowledge factors within the given set. Though the calculation differs barely while you’re taking a look at a pattern versus inhabitants, you may calculate the variance as the typical of the squared variations from the imply.

Because the variance is a squared worth, it may be tough to interpret in comparison with different measures of variability like commonplace deviation. Regardless, reviewing variance will be useful; doing so could make it simpler so that you can determine which statistical assessments to make use of together with your knowledge. Relying on the statistical assessments, uneven variance between samples may skew or bias outcomes.

One of many well-liked statistical assessments that applies variance known as the evaluation of variance (ANOVA) check. An ANOVA check is used to gauge whether or not any of the group means are considerably totally different from each other when analyzing a categorical impartial variable and a quantitative dependent variable. For instance, say you wish to analyze whether or not social media use impacts hours of sleep. You can break social media use into totally different classes like low use, medium use and excessive use, then run an ANOVA check to gauge whether or not there are statistical variations between the group means. The check can present whether or not outcomes are defined by group variations or particular person variations.

How do you discover the variance?

Calculating the variance for an information set can differ primarily based on whether or not the set is all the inhabitants or a pattern of the inhabitants.

The system for calculating the variance of a whole inhabitants appears to be like like this:

σ² = ∑ (Xᵢ— μ)² / N

A proof of the system:

• σ² = inhabitants variance
• Σ = sum of…
• Χᵢ = every worth
• μ = inhabitants imply
• Ν = variety of values within the inhabitants
• Utilizing an instance vary of numbers, let’s stroll by way of the calculation step-by-step.

Instance vary of numbers: 8, 6, 12, 3, 13, 9

Discover the inhabitants imply (μ):

Calculate deviations from the imply by subtracting the imply from every worth.

Sq. every deviation to get a optimistic quantity.

Sum the squared values.

Divide the sum of squares by N or n-1.

Since we’re working with all the inhabitants, we’ll divide by N. If we have been working with a pattern of the inhabitants, we might divide by n-1.

69.5/6 = 11.583

There we now have it! The variance of our inhabitants is 11.583.

Why use n-1 when calculating the pattern variance?

Making use of n-1 to the system known as Bessel’s correction, named after Friedrich Bessel. When utilizing samples, we have to calculate the estimated variance for the inhabitants. If we used N as a substitute of n-1 for the pattern, the estimate can be biased, doubtlessly underestimating the inhabitants variance. Utilizing n-1 will make the variance estimate bigger, overestimating variability in samples, thus lowering biases.

Let’s recalculate the variance pretending the values are from a pattern:

As we are able to see, the variance is bigger!

Calculating variance utilizing Python

Now that we’ve executed the calculation by hand, we are able to see that finishing it for a big set of values can be very tedious. Fortunately, Python can simply deal with the calculation for very massive knowledge. We are going to discover two strategies utilizing Python:

• Write our personal variance calculation perform
• Use Pandas’ built-in perform

Writing a variance perform

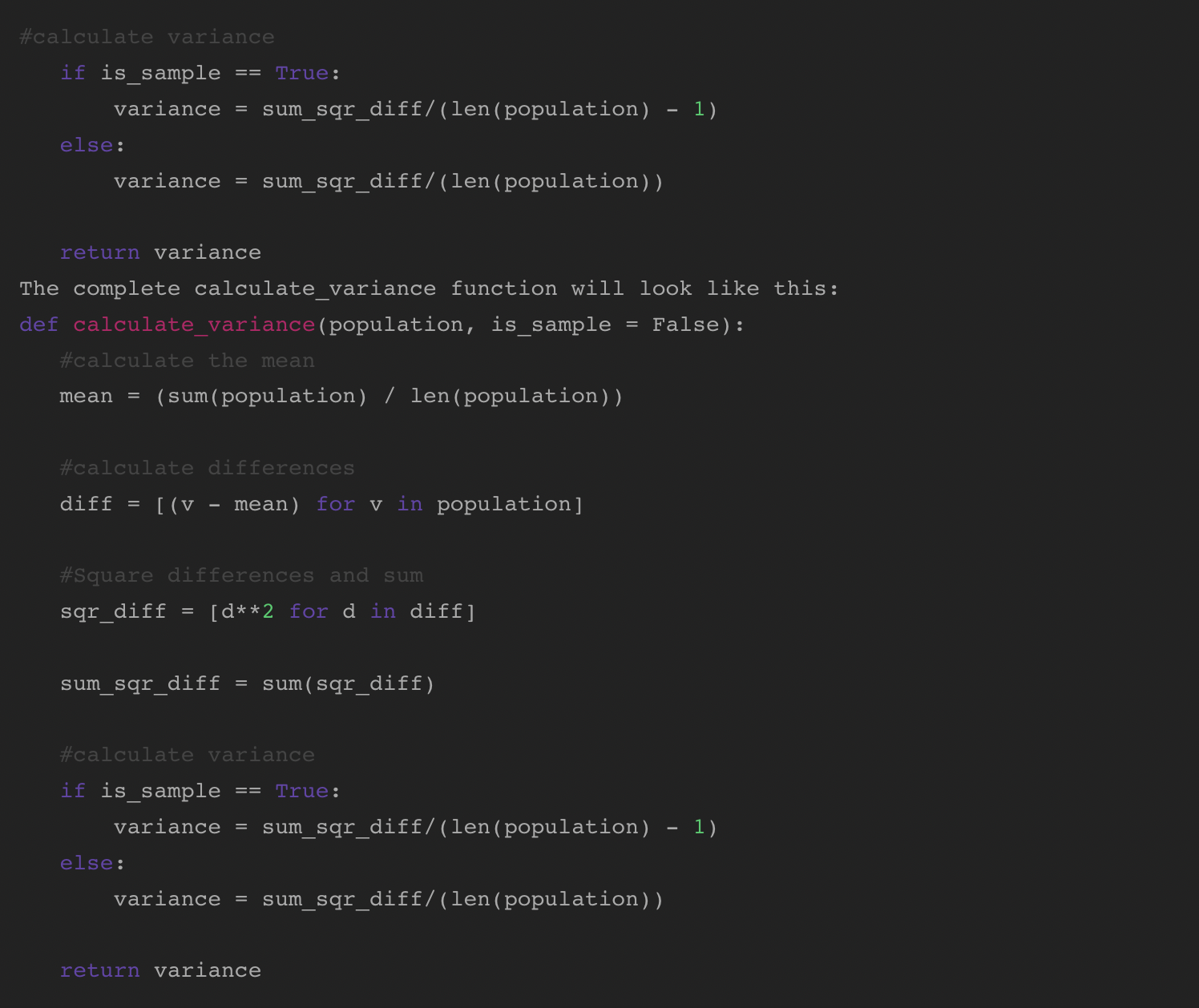
As we start to jot down a perform to calculation variance, assume again to the steps we took when calculating by hand. We wish the perform to soak up two parameters:

• inhabitants: an array of numbers
• is_sample: a Boolean to change the calculation relying on whether or not we’re working with a pattern or inhabitants

Begin by defining the perform that takes within the two parameters.

Subsequent, add logic to calculate the inhabitants imply.

After calculating the imply, discover the variations from the imply for every worth. You are able to do this in a single line utilizing a listing comprehension.

Subsequent, sq. the variations and sum them.

Lastly, calculate the variance. Utilizing an If/Else assertion, we are able to make the most of the is_sampleparameter. If is_sampleis true, calculate variance utilizing (n-1). Whether it is false (the default), use N:

We are able to check the calculation utilizing the vary of numbers we crunched by hand:

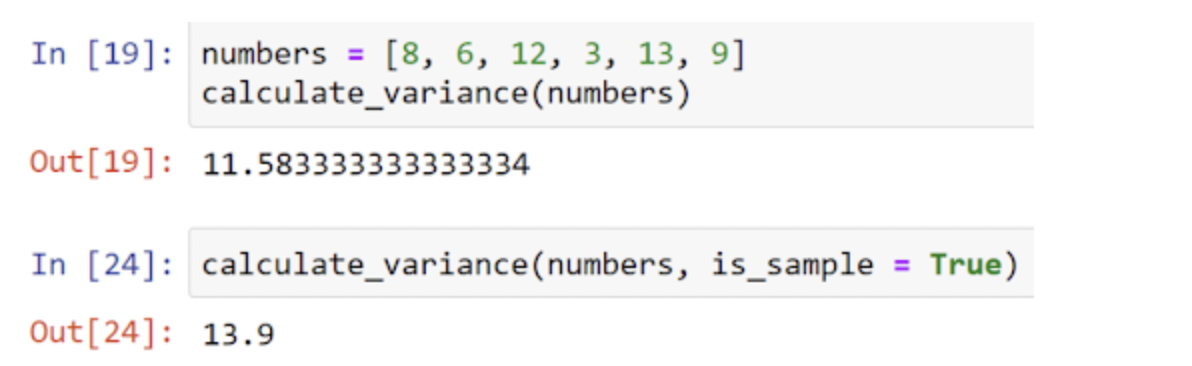
Discovering variance utilizing Pandas

Though we are able to write a perform to calculate variance in lower than 10 strains of code, there’s an excellent simpler technique to discover variance. You are able to do it in a single line of code utilizing Pandas. Let’s load up some knowledge and work by way of an actual instance of discovering variance.

Loading instance knowledge

The Pandas instance makes use of the BMW Worth Problem knowledge set from Kaggle, which is free to obtain. Start by importing the Pandas library, after which studying the CSV file right into a Pandas knowledge body:

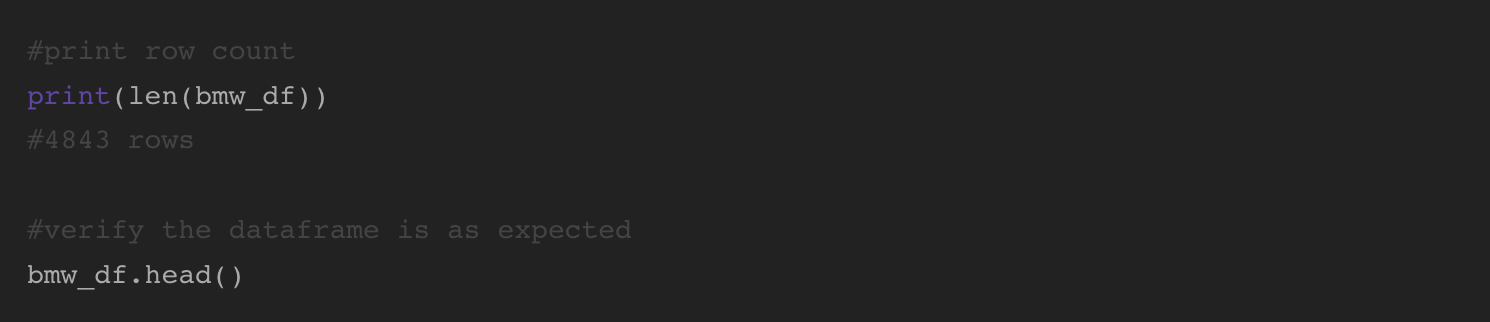
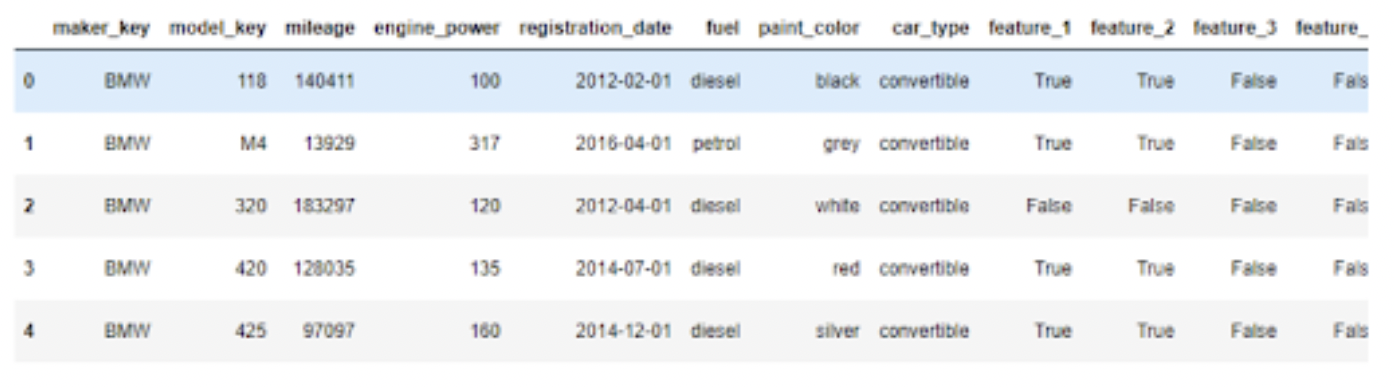
We are able to depend the variety of rows within the knowledge set and show the primary 5 rows to ensure all the things loaded appropriately:

Discovering the variance for the BMW knowledge

Because the BMW knowledge set is 4843 rows, calculating that by hand would…not be enjoyable. As an alternative we are able to merely plug within the column from the info body into our calculate_variance perform and return the variance. Let’s discover the variance for the numeric columns mileage, engine_power and value.

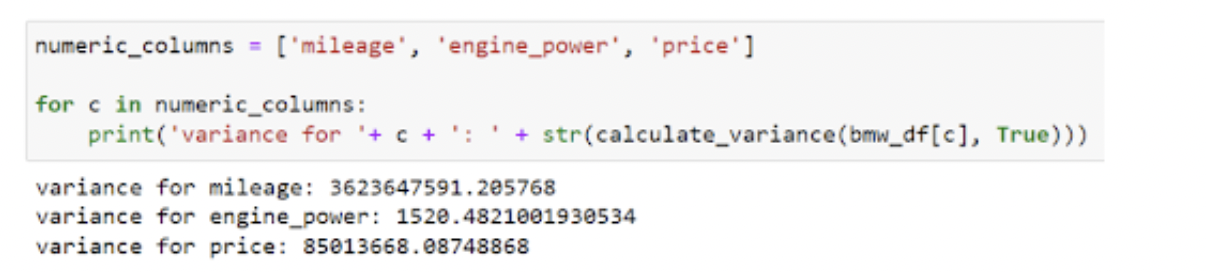
Utilizing Pandas var() perform

In case we neglect the calculation for variance and can’t write our personal perform, Pandas has a built-in perform to calculate variance named var(). By default, it assumes a pattern inhabitants and makes use of n-1 within the calculation; nevertheless, you may regulate the calculation by passing within the ddof=0 argument.

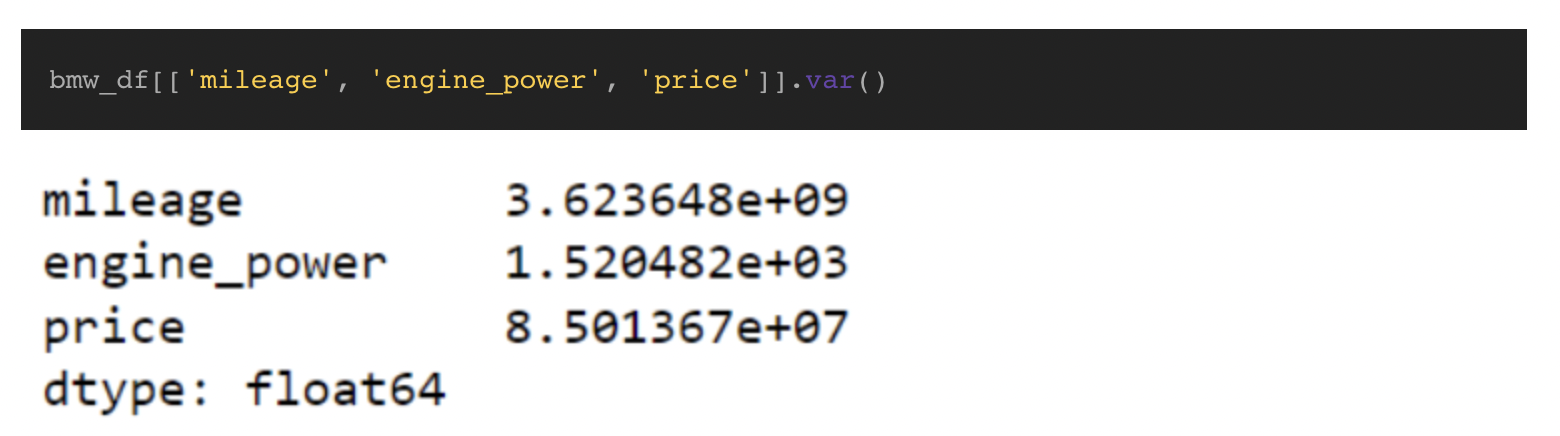
As we are able to see the Var() perform matches the values produced by our calculate_variance perform, and it’s just one line of code. Reviewing the outcomes, we are able to see mileage has a excessive variance which means the values are likely to range from the imply by quite a bit. That is sensible as a result of many elements play into the space an individual must drive. By comparability, engine_power has a low variance which signifies the values don’t range extensively from the imply.

The takeaway

Understanding variance will be an essential a part of knowledge evaluation and machine studying as a result of you should utilize it to evaluate group variations. Variance additionally impacts which statistical assessments can assist us make knowledge pushed selections. Excessive variance means values are drastically dispersed from the imply, whereas low variance means numbers usually are not extensively dispersed from the imply. If we now have a small set of values, it’s attainable to calculate the variance by hand in solely 5 steps. For giant knowledge units, we noticed how easy it’s to calculate variance utilizing Python and Pandas. The Var() perform in Pandas calculates the variance for the numerical columns in an information body in just one line of code, which is fairly helpful!